#1 교육정리
오늘은 아래와 같이 학습한 내용을 정리해보겠습니다.
퍼셉트론의 과제SVM(Support Vector Machine)Decision TreeRandom ForestBoosting 계열의 모델K-FoldScaling
#2 퍼셉트론의 과제
퍼셉트론이 완성되고 아달라인에 의해 보완되며 드디어 현실 세계의 다양한 문제를 해결하는 인공지능이 개발될 것으로 기대했습니다. 하지만 곧 퍼셉트론의 한계가 보고됩니다. 퍼셉트론의 한계가 무엇이었는지 알고 이를 극복하는 과정을 이해하는 것은 우리에게도 매우 중요합니다. 이것을 해결한 것이 바로 딥러닝이기 때문입니다.
사각형 종이에 검은색 점 두 개와 흰색 점 두 개가 놓여 있습니다. 이 네 점 사이에 직선을 하나 긋는다고 합시다. 이때 직선의 한쪽 편에는 검은색 점만 있고, 다른 한쪽에는 흰색 점만 있게끔 선을 그을 수 있을까요?
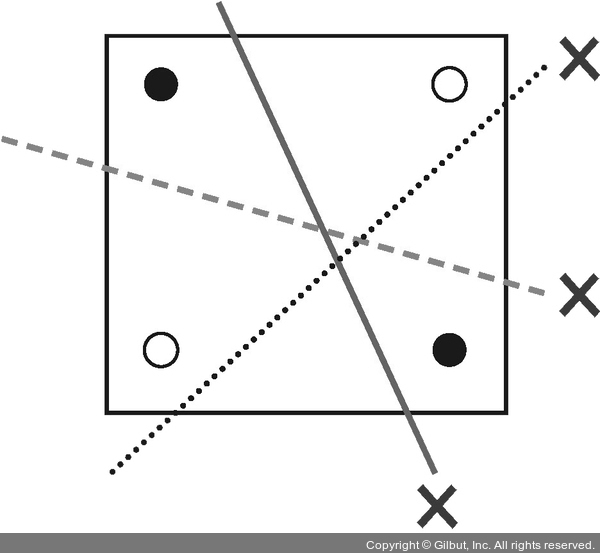
그림 7-4 | 선으로는 같은 색끼리 나눌 수 없다: 퍼셉트론의 한계
선을 여러 개 아무리 그어 보아도 하나의 직선으로는 흰색 점과 검은색 점을 구분할 수 없습니다.
퍼셉트론이나 아달라인은 모두 2차원 평면상에 직선을 긋는 것만 가능합니다. 이 예시는 경우에 따라 선을 아무리 그어도 해결되지 않는 상황이 있다는 것을 말해 줍니다.
이것이 퍼셉트론의 한계를 설명할 때 등장하는 XOR(exclusive OR) 문제입니다.
XOR 문제는 논리 회로에 등장하는 개념입니다. 컴퓨터는 두 가지의 디지털 값, 즉 0과 1을 입력해 하나의 값을 출력하는 회로가 모여 만들어지는데, 이 회로를 ‘게이트(gate)’라고 합니다.
그림 7-5는 AND 게이트, OR 게이트, XOR 게이트에 대한 값을 정리한 것입니다. AND 게이트는 x1과 x2 둘 다 1일 때 결과값이 1로 출력됩니다. OR 게이트는 둘 중 하나라도 1이면 결괏값이 1로 출력됩니다. XOR 게이트는 둘 중 하나만 1일 때 1이 출력됩니다.
| AND (논리곱) 두 개 모두 1일 때 1 |
OR (논리합) 두 개 중 한 개라도 1이면 1 |
XOR (배타적 논리합) 하나만 1이어야 1 |
||||||||
| x1 | x2 | 결괏값 | x1 | x2 | 결괏값 | x1 | x2 | 결괏값 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | ||
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | ||
그림 7-5 | AND, OR, XOR 게이트에 대한 진리표
그림 7-5를 각각 그래프로 좌표 평면에 나타내 보겠습니다. 결괏값이 0이면 흰색 점으로, 1이면 검은색 점으로 나타낸 후 조금 전처럼 직선을 그어 위 조건을 만족할 수 있는지 보겠습니다.

그림 7-6 | AND, OR, XOR 진리표대로 좌표 평면에 표현한 후 선을 그어 색이 같은 점끼리 나누기(XOR는 불가능)
AND와 OR 게이트는 직선을 그어 결괏값이 1인 값(검은색 점)을 구별할 수 있습니다. 그러나 XOR의 경우 선을 그어 구분할 수 없습니다.
이는 인공지능 분야의 선구자였던 MIT의 마빈 민스키(Marvin Minsky) 교수가 1969년에 발표한 “퍼셉트론즈(Perceptrons)”라는 논문에 나오는 내용입니다.
‘뉴런 → 신경망 → 지능’이라는 도식에 따라 ‘퍼셉트론 → 인공 신경망 → 인공지능’이 가능하리라 꿈꾸었던 당시 사람들은 이것이 생각처럼 쉽지 않다는 사실을 깨닫게 됩니다. 알고 보니 간단한 XOR 문제조차 해결할 수 없었던 것입니다. 이 논문 이후 인공지능 연구가 한동안 침체기를 겪게 됩니다. 이 문제는 두 가지 방법이 순차적으로 개발되면서 해결됩니다. 하나는 다층 퍼셉트론(multilayer perceptron), 그리고 또 하나는 오차 역전파(back propagation)입니다.
#3 SVM(Support Vector Machine) model
서포트 벡터 머신은 여백(Margin)을 최대화하여 일반화 능력을 극대화 하는 지도 학습알고리즘입니다. 여백은 주어진 데이터가 오류를 발생시키지 않고 움직일 수 있는 최대 공간입니다. 분류를 위한 서포트 벡터 머신 : SVC, 회귀를 위한 서포트 벡터 머신 : SVR 이 있습니다.

그 두 부류 사이의 여백이 가장 넓어지면(둘이 가장 떨어져 있으면(=margin최대화)) 그 둘을 가장 잘 분류했다고 할 수 있다.
이를 분류하는 과정은 위의 그래프와 같이 빨간 직선(선형모델)으로 그 둘을 구분 할 수도 있고 때에 따라서는 구불구불한 곡선으로(비선형모델)으로 둘을 구분할 수 있을 것이다. 이렇게 직관적으로는 어려운 이야기가 아니지만 실제 이론으로 정리하는 일은 쉽지 않다.
decision rule)
가중치 벡터 w와 직교하면서 margin이 최대가 되는 선형을 찾는다. 이 말이 받아들이기 어렵다면 위의 그림을 좀 더 수학적으로 표현한 아래의 그래프를 통해 이해해보자.

- support vector:두 가지 카테고리에 각각 해당되는 data set들('-'샘플이 모인곳/'+'샘플이 모인곳)의 최외각에 있는 샘플들을 support vector라고 부른다. 이 가장 최 외각에 있는 벡터들을 토대로 margin M을 구할 수 있기 때문에 중요한 벡터들이다.
- margin: support vector를 통해 구한 두 카테고리 사이의 거리를 m이라고 하고 이를 최대화 해야한다.
우리가 가진 '+'샘플과 '-'샘플을 구분하기 위해 support vector를 통해 margin이 최대가 되는 빨간점선을 만들려고 한다.
'+'샘플과 '-'샘플들은 선형으로 분리가 가능한 상황이다. 그러므로 직선을 통해 두 dataset을 분리하도록 하자. 이 때 이 직선을 결정 초평면(decision hyperline)부르기로 한다. 결정 초평면을 정의하기 위해서는 두 개의 매개변수가 필요하다. 결정 초평면에 수직하는 가중치벡터 w와 상수 b이다.
SVC & SVR)
- SVC (Support Vector Classification):
- SVC는 지도 학습에서 분류(Classification)를 수행하는 알고리즘입니다.
- 이 알고리즘은 주어진 데이터를 가장 잘 나누는 결정 경계(Decision Boundary)를 찾는 것이 목표입니다.
- 데이터 포인트들을 고차원 공간으로 매핑하여 결정 경계를 찾습니다.
- 서포트 벡터(Support Vector)라 불리는 데이터 포인트들을 이용하여 결정 경계를 정의하고, 그 경계로부터 가장 멀리 떨어진 데이터 포인트들을 찾습니다.
- 이러한 서포트 벡터들을 기반으로 새로운 데이터 포인트들을 분류합니다.
- SVR (Support Vector Regression):
- SVR은 지도 학습에서 회귀(Regression)를 수행하는 알고리즘입니다.
- 회귀 분석에서는 연속적인 값을 예측하는 것이 목표입니다.
- SVR은 분류와 유사하게 데이터 포인트들을 고차원 공간으로 매핑하여 회귀를 수행합니다.
- 학습 데이터와의 편차를 최소화하는 초평면(Hyperplane)을 찾습니다.
- 초평면으로부터 허용 오차 범위 내에서 최대한 많은 데이터 포인트들이 위치하도록 합니다.
- 이후, 새로운 데이터 포인트들에 대한 예측은 초평면에서의 함수값으로 이루어집니다.
SVC와 SVR은 모두 기계 학습 문제에 활용되며, 데이터 분류와 회귀 작업을 수행하는 데 유용합니다.
#4 Decision Tree
분류 및 회귀 에 사용되는 비모수 지도 학습 방법입니다 . 목표는 데이터 특성에서 유추된 간단한 결정 규칙을 학습하여 대상 변수의 값을 예측하는 모델을 만드는 것입니다. 트리는 조각별 상수 근사치로 볼 수 있습니다.
예를 들어, 아래 예에서 의사 결정 트리는 일련의 if-then-else 결정 규칙을 사용하여 사인 곡선을 근사화하기 위해 데이터에서 학습합니다. 트리가 깊을수록 결정 규칙이 더 복잡해지고 모델이 더 적합해집니다.

장점)
1. 이해하고 해석하기 쉽습니다. 나무를 시각화할 수 있습니다.
2. 트리를 사용하는 비용(즉, 데이터 예측)은 트리를 훈련하는 데 사용되는 데이터 포인트의 수에서 대수적입니다.
3. 숫자 및 범주 데이터를 모두 처리할 수 있습니다.
4. 다중 출력 문제를 처리할 수 있습니다.
5. 통계 테스트를 사용하여 모델을 검증할 수 있습니다. 이를 통해 모델의 신뢰성을 설명할 수 있습니다
6. 데이터가 생성된 실제 모델에 의해 가정이 다소 위반되는 경우에도 잘 수행됩니다.
단점)
1. 결정 트리 학습자는 데이터를 잘 일반화하지 못하는 지나치게 복잡한 트리를 만들 수 있습니다. 이를 과적합이라고 합니다. 이러한 문제를 피하기 위해서는 가지치기, 리프 노드에 필요한 최소 샘플 수 설정 또는 트리의 최대 깊이 설정과 같은 메커니즘이 필요합니다.
2. 데이터의 작은 변화로 인해 완전히 다른 트리가 생성될 수 있으므로 의사 결정 트리가 불안정할 수 있습니다. 이 문제는 앙상블 내에서 결정 트리를 사용하여 완화됩니다.
3. 의사결정 트리의 예측은 순조롭거나 연속적이지 않지만 위의 그림에서 볼 수 있는 것처럼 구분적으로 일정한 근사입니다. 따라서 외삽법이 좋지 않습니다.
4. 최적의 의사 결정 트리를 학습하는 문제는 최적의 여러 측면과 단순한 개념에서도 NP-완전인 것으로 알려져 있습니다. 결과적으로 실용적인 결정 트리 학습 알고리즘은 각 노드에서 로컬로 최적의 결정이 내려지는 그리디 알고리즘과 같은 휴리스틱 알고리즘을 기반으로 합니다. 이러한 알고리즘은 전역적으로 최적의 의사 결정 트리를 반환한다고 보장할 수 없습니다. 이는 앙상블 학습기에서 여러 트리를 훈련하여 완화할 수 있습니다. 이 경우 기능과 샘플이 교체를 통해 무작위로 샘플링됩니다.
5. XOR, 패리티 또는 멀티플렉서 문제와 같이 결정 트리가 쉽게 표현하지 못하기 때문에 배우기 어려운 개념이 있습니다.
6. 결정 트리 학습자는 일부 클래스가 우세한 경우 편향된 트리를 생성합니다. 따라서 의사 결정 트리에 맞추기 전에 데이터 세트의 균형을 맞추는 것이 좋습니다.

출처 : https://ratsgo.github.io/machine%20learning/2017/03/26/tree/
#5 Random Forest
과적합(overfitting) 을 방지하기 위해, 최적의 기준 변수를 랜덤하게 선택하는 breiman(2001)이 제안한 머신러닝 기법이다. Random Forest는 랜덤으로 일부 feature만을 선택하여 Decision tree (의사결정나무)를 만들고, 해당 과정을 반복하여 여러개의 Decision tree를 형성합니다.
여러 개의 Decision tree에서 나온 예측값을 토대로 가장 많이 나온 값을 최종 예측값으로 선정합니다. 최종 예측값을 산정하는 방법에서 분류모델은 가장 많이 등장한 값을 선택하고 회귀일 경우 평균값을 많이 사용합니다.
Random Forest처럼 여러 개의 결과를 합쳐 최종 결과를 도출하는 방식을 앙상블 (Ensemble) 모델이라고 합니다.

이미지 출처 : https://www.tibco.com/ko/reference-center/what-is-a-random-forest
장점)
1. Classification 및 Regression 문제에 모두 사용 가능
2. 대용량 데이터 처리에 효과적
3. 과대적합 문제 최소화하여 모델의 정확도 향상
단점)
1. 랜덤 포레스트 특성상 데이터 크기에 비례해서 수백개에서 수천개의 트리를 형성하기에 예측에 오랜 프로세스 시간이 걸림
2. 랜덤 포레스트 모델 특성상 생성하는 모든 트리 모델을 다 확인하기 어렵기에 해석 가능성이 떨어짐.
구축)

이미지 출처 : https://bioinformaticsandme.tistory.com/167
1) 랜덤포레스트 모델을 만들기 위해 생성할 트리의 개수를 지정 (bootstrap sampling(부트스트랩 샘플링) - Original sample 집단에서 더 작지만, 무수히 많은 집단으로 랜덤하게 뽑는 방법)
- 각 트리는 고유하게 무작위적으로 선택해서 만들어 짐
- n_samples 개의 데이터 포인트 중에서 n_samples 횟수만큼 반복 추출 (한 표본이 여러 번 중복으로 추출될 수 있음)
- 추출한 데이터 세트는 원래 데이터 세트 크기와 같지만, 어떤 데이터 포인트는 누락 될 수 있고(대략 1/3), 어떤 데이터 포인트는 중복되어 들어 있을 수 있음
- 뽑은 데이터 세트로 결정 트리를 만듦
- 트리의 분기마다 feature을 사용 (몇 개의 feature를 고를지는 max_features로 조정); max feature 값 클수록 트리들은 비슷해지고, 낮출수록 트리들은 많이 달라지고 각 트리는 데이터에 맞추기 위해 깊이가 깊어짐
2) Bootstrap sample에 대해 Random Forest Tree 모형 제작
- 전체 변수 중에서 m개 변수를 랜덤하게 선택
- 최적의 classifier 선정
- classifier 따라 두 개의 daughter node 생성
3) Tree 들의 앙상블 학습 결과 출력
대안책 - XGBoost)
XGBoost는 Random Forest와 유사하게 여러 개의 의사결정나무를 이용한 앙상블 모델입니다. 하지만, XGBoost는 Random Forest와의 성능 차이를 위해 Boosting 방법을 이용하여 구현되었습니다. 참고로 Random Forest는 Bagging 방법을 이용하여 구현되었습니다. 또한, XGBoost는 Gradient Boosting 대비 빠른 수행시간을 가졌고 분류와 회귀 두 영역에서 아주 효율적인 예측 성능을 발휘하고 있어 산업 부분에서도 널리 사용되고 있습니다.
글참고 출처 : http://www.incodom.kr/Random_Forest
#6 Boosting 계열의 모델
boosting이란)
Boosting이란 약한 분류기를 결합하여 강한 분류기를 만드는 과정
부스팅은 약한 모델을 결합하면 임의의 강한 모델의 성능 이상으로 끌어올릴(Boosting) 수 있지 않을까 하는 아이디어에서 시작되었습니다. 먼저 약한 모델을 만든 후에 학습 결과를 바탕으로 이를 보완해 줄 수 있는 모델을 반복해서 생성합니다
각 0.3의 정확도를 가진 A, B, C를 결합하여 더 높은 정확도
예를 들어 0.7 정도의 accuracy를 얻는 게 앙상블 알고리즘의 기본 원리
Boosting은 이 과정을 순차적으로 실행 A 분류기를 만든 후, 그 정보를 바탕으로 B 분류기를 만들고, 다시 그 정보를 바탕으로 C 분류기를 만듭니다.

Adaboost)
Adaboost는 여러 부스팅 알고리즘 중에서 초기에 사용된 알고리즘 중 하나입니다. 해당 알고리즘은 틀리게 예측한 인스턴스에 가중치(Weight)를 부여한다는 아이디어를 기본으로 하고 있습니다. 특이한 점은 이진 분류 문제에서 레이블을 0,10,1 이 아니라 −1,1−1,1 로 구분한다는 것인데요. 이는 서포트 벡터 머신에서도 그랬듯이 알고리즘에서 사용되는 수식 때문입니다
다수결을 통한 정답 분류 및 오답에 가중치를 부여 합니다.
자세한 함수 설명 참고 : https://yngie-c.github.io/machine%20learning/2021/03/20/adaboost/
GBM-Gradient Boosting Machine)
GBM의 학습방법 역시 AdaBoost와 유사하지만, 경사 하강법(Gradient Descent)을 이용해 가중치를 업데이트한다는 점에서 차이가 있습니다.
GBM은 CART(Classification and Regression Trees) 기반의 다른 알고리즘과 마찬가지로 분류뿐만 아니라 회귀도 수행할 수 있습니다.
GBM은 이처럼 많은 장점이 있지만, 과적합 규제 기능이 없다는 단점이 있습니다.
경사하강법이란(Gradient Descent) :
경사 하강법은 경사 즉 기울기를 줄여나감으로써 오류를 최소화하는 방법을 의미합니다.
실제값과 모델의 예측값 차이에 따른 오류값을 잔차(Residual)라고 합니다.
이러한 잔차의 제곱합인 RSS(Residual Sum of Square)를 비용 함수 또는 손실 함수(loss function)이라고 부르는데요.
머신러닝 알고리즘은 이 비용 함수 값을 지속적으로 감소시켜 최종적으로 더 이상 감소하지 않는 최소의 오류값을 구하는 방향으로 학습이 이뤄집니다.
경사 하강법도 머신러닝 알고리즘의 학습과 유사한 방식입니다.
비용 함수(오류식)에 미분을 적용한 뒤 이 미분값이 계속 감소하는 방향으로 파라미터 w를 조정하다가, 미분값이 더이상 감소하지 않는 지점을 비용 함수가 최소인 지점으로 간주하고 그때의 파라미터 w를 반환하는 것입니다.
쉽게 말해 경사=기울기(Gradient)=손실함수의 미분계수이며 이 값이 0인 지점을 찾아가는 것입니다.

출처 : https://dacon.io/en/competitions/official/235946/codeshare/5623
LightGBM)
Light GBM은 말 그대로 “Light” 가벼운 것인데요, 이유는 속도가 빠르기 때문입니다.
Light GBM은 큰 사이즈의 데이터를 다룰 수 있고 실행시킬 때 적은 메모리를 차지합니다. Light GBM이 인기있는 또 다른 이유는 바로 결과의 정확도에 초점을 맞추기 때문입니다.
LGBM은 또한 GPU 학습을 지원하기 때문에 데이터 사이언티스트가 데이터 분석 어플리케이션을 개발할 때 LGBM을 폭넓게 사용하고 있습니다.
LGBM을 작은 데이터 세트에 사용하는 것은 추천되지 않습니다. Light GBM은 overfitting (과적합)에 민감하고 작은 데이터에 대해서 과적합하기 쉽습니다. row (행) 수에 대한 제한은 없지만 제 경험상 10,000 이상의 row (행) 을 가진 데이터에 사용하는 것을 권유해드립니다.
Light GBM은 Tree가 수직적으로 확장되는 반면에 다른 알고리즘은 Tree가 수평적으로 확장됩니다. 즉 Light GBM은 leaf-wise입니다.
최대 손실 값(Max data loss)을 가지는 리프 노트를 지속적으로 분할하면서 트리의 깊이가 깊어지고 비대칭적인 트리가 생성됩니다. 그런데 최대 손실값을 가지는 리프 노드를 반복할수록 결국은 균형 트리의 분할 방식보다 예측 오류 손실을 최소화 할 수 있습니다

XGBoost)
XGBoost는 Extreme Gradient Boosting의 약자입니다.
Boosting 기법을 이용하여 구현한 알고리즘은 Gradient Boost 가 대표적인데
이 알고리즘을 병렬 학습이 지원되도록 구현한 라이브러리가 XGBoost 입니다.
Regression, Classification 문제를 모두 지원하며, 성능과 자원 효율이 좋아서, 인기 있게 사용되는 알고리즘이다.
장점으로는 아래와 같은 장점이 있습니다.
- GBM 대비 빠른 수행시간, 병렬 처리로 학습, 분류 속도가 빠르다.
- 과적합 규제(Regularization), 표준 GBM 경우 과적합 규제기능이 없으나, XGBoost는 자체에 과적합 규제 기능으로 강한 내구성 지닌다.
- 분류와 회귀영역에서 뛰어난 예측 성능 발휘 즉, CART(Classification and regression tree) 앙상블 모델을 사용
- Early Stopping(조기 종료) 기능이 있음
- 다양한 옵션을 제공하며 Customizing이 용이하다.
CATBoost)
Catboost 역시 마찬가지로 속도 개선 로직과 정규화 방법을 보유하고 있는 Boosting류 모델입니다.
유명한 Boosting계열 모델 중 하나인 XGBoost와 Catboost가 유사한 점이라면 두 모델의 가장 큰 차이점은 트리를 boosting해나가는 방향이 같습니다. 두 모델은 level-wise로 트리를 만들어나갑니다.
*level-wise란 : 트리를 만들 때 두 가지 방향으로 확장해나갈 수 있습니다. 하나는 level-wise, 즉 옆으로 확장하는 방법과 leaf-wise인 밑으로의 확장방식이 있습니다.
Catboost 는 기존의 boosting 과정과 가장 다른 점이 있습니다. 기존의 Boosting 모델들은 모든 훈련 데이터를 대상으로 잔차계산을 했지만 Catboost 는 학습데이터의 일부만으로 잔차계산을 한 뒤, 이 결과로 모델을 다시 만들게 됩니다.
Catboost는 이름에서도 유추 가능하듯이 Cat, Category 즉 범주형 변수가 많은 데이터를 학습할 때 성능이 좋은 것으로 알려져있습니다. Response encoding과 Categorical Feature Combination이라고 하여 두 방법이 범주형 변수를 효율적으로 처리하는데 큰 장점이 됩니다.
수치형 변수는 다른 일반 트리 모델과 동일하게 처리한다고 합니다. 분기가 발생하면 Gain, 즉 정보의 획득량이 높은 방향대로 나뉘게 됩니다. 수치형 변수가 많게 되면 lightGBM 모델처럼 시간이 오래 걸리고 따라서 범주형 변수가 많을 때 이 모델을 사용하기를 추천합니다. 또한 Sparse한 matrix는 적용하기 어렵다고 합니다.
Catboost는 시계열 데이터를 효율적으로 처리하는 것으로 알려져있습니다.
또 속도가 매우 빨라 실제 상용화되고 있는 서비스에 예측 기능을 삽입하고자 할 때 효과적일 수 있고 XGBoost보다 예측 속도가 8배 빠르다고 알려져있습니다.
imbalanced dataset도 class_weight 파라미터 조정을 통해 예측력을 높일 수도 있습니다.
그 외 Catboost는 오버피팅을 피하기 위해 내부적으로 여러 방법(random permutation, overfitting detector)을 갖추고 있어 속도 뿐만 아니라 예측력도 굉장히 높습니다.
아래 그림은 대표적인 public ML dataset의 테스트 데이터셋으로 log-loss를 계산한 값입니다.
보다싶이 Catboost 모델이 가장 낮은 값을 보이고 있습니다.

출처 : https://julie-tech.tistory.com/119
#7 K-Fold(교차검증)
흐름)

머신러닝 학습 시 최적의 파라메터를 찾는 것은 중요한 이슈라고 할 수 있습니다. 실제로 캐글과 같은 경연 플랫폼에서는 파라메터 세팅이 조금만 달라도 결과가 달라지고 이것은 순위의 변동으로도 이어집니다.
머신러닝 모델에서 가장 보편적으로 사용되는 교차 검증 기법입니다.
위 그림 속 CV 흐름도를 요약하자면
- CV(교차검증)를 실시하여 여러 머신러닝 기법 모델의 전반적인 성능을 비교한 후 하나의 기법을 선택
- 선택된 기법을 활용하여 데이터에 알맞은 최적의 파라메터 탐색
단계 순서)

- 데이터의 상황에 따라 K개의 Group으로 알맞게 나눔
- K-1개 그룹의 데이터를 훈련 데이터로 사용하여 모델을 훈련
- 데이터의 나머지 부분에 대해 검증 (즉, 정확도와 같은 성능 측정값을 계산하는 데 테스트 세트로 사용됨)
- 검증 데이터 그룹을 달리하여 2,3 과정을 반복 (즉, 총 K번의 검증이 이루어짐)
- K번 검증된 결과의 평균을 측정 (예를 들면 K번의 정확도 결과를 평균냄)
* 해당 과정에서 중요한 점은 Data Leakage가 없도록 훈련 데이터와 검증 데이터를 명확히 구분해야 한다는 점이다.
출처 : https://jonsyou.tistory.com/23
#8 스케일링(Scaling)
스케일링이란)
- 데이터 전처리 과정 중 하나(data scaling/feature scaling)
- ex) x는 0부터 1사이의 값을 갖고, y는 10부터 100사이의 값을 갖는다고 가정하면, x의 특성은 y를 예측하는데 큰 영향을 주지 않을 수 있습니다.
- 때문에 특성별로 데이터의 스케일이 다르다면, ML이 잘 동작하지 않을 수 있습니다.
- 따라서 데이터 스케일링 작업을 통해 모든 특성의 범위 또는 분포를 같게 만들어줘야 합니다.
분류)
1) StandardScaler() :
- 특성들의 평균을 0, 분산을 1로 스케일링, 특성들을 (표준)정규분포로 만드는 것
- 최솟값과 최댓값의 크기를 제한하지 않기 때문에, 어떤 알고리즘에서는 문제가 있을 수 있음
- 평균과 표준편차가 이상치로부터 영향을 많이 받는다는 점에서 이상치에 매우 민감
- 회귀보다 분류에 유용
- 모든 피쳐들이 같은 스케일을 갖게 됨
- Standardization의 궁극적인 목표는 모든 피쳐들을 공통의 척도로 변경해주는 것, 즉 값의 범위의 차이를 왜곡하지 않으면서 모든 피쳐를 공통의 척도로 스케일해주는 것
2) MinMaxScaler() :
- Min-Max Normalization
- 특성들을 특정 범위(주로 [0,1])로 스케일링, 가장 작은 값은 0, 가장 큰 값은 1로 변환되므로, 모든 특성들은 [0,1] 범위를 갖게 됨
- 이상치에 매우 민감
- 분류보다 회귀에 유용
- (x - (x의 최솟값)) / ((x의 최댓값) - (x의 최솟값)
- 데이터의 최솟값과 최댓값을 알 때 사용
- 이상치가 존재할 경우 스케일링 결과가 매우 좁은 범위로 압축될 수 있음
3) MaxAbsScaler() :
- 각 특성의 절대값이 0과 1 사이가 되도록 스케일링
- 모든 값은 -1과 1 사이로 표현되며, 데이터가 양수일 경우 MinMaxScaler와 유사하게 동작
- 이상치에 매우 민감, 이상치가 큰 쪽에 존재할 경우 이에 민감할 수 있음
4) RobustScaler() :
- 평균과 분산 대신에 중간값과 사분위값을 사용(중간값은 정렬시 중간에 있는 값, 사분위값은 1/4, 3/4에 위치한 값)
- 이상치 영향을 최소화하여 정규분포보다 더 넓게 분포
- RobustScaler()를 사용할 경우 StandardScaler()에 비해 스케일링 결과가 더 넓은 범위로 분포
- 모든 피쳐들이 같은 스케일을 갖게 됨
5) Normalizer() :
- 앞의 4가지 스케일러는 각 특성/열의 통계치를 이용하여 진행되는데, Normalizer의 경우 각 샘플/행마다 적용되는 방식
- 한 행의 모든 특성들 사이의 유클리드 거리(L2 norm)가 1이 되도록 스케일링
- 일반적인 데이터 전처리의 상황에서 사용되는 것이 아니라, 모델, 특히 딥러닝 내 학습 벡터에 적용하며, 특히나 피쳐들이 다른 단위(키, 나이, 소득 등)라면 더더욱 사용하지 않음
scikit-learn 에서의 scaling)
- scaler는 fit와 transform 메서드를 지니고 있는데, fit 메서드는 훈련 데이터에만 적용해, 훈련 데이터의 분포를 먼저 학습하고, 그 이후 transform 메서드를 훈련 데이터와 테스트 데이터에 적용해 스케일을 조정해야 함
- 따라서, 훈련 데이터에는 fit_transform() 메서드를 적용하고, 테스트 데이터에는 transform() 메서드를 적용해야 함(fit_transform()은 fit과 transform이 결합된 단축 메서드)
- 스케일링할 때, 모든 특성의 범위를 유사하게 만드는 것은 중요하지만, 그렇다고 모두 같은 분포로 만들 필요는 없음, 특성에 따라 각기 다른 스케일링을 적용하는게 유리할 수도 있기 때문
- scaler.fit() : 데이터 변환을 학습, train셋에 대해서만 적용
- scaler.transform() : 실제로 데이터 변환을 모두 수행, train셋과 test셋 모두에 대해서 적용
- 만약 fit_transform을 test data에도 적용하게 되면 test data로부터 새로운 평균값과 분산값을 얻게 됨, 즉 모델이 test data도 학습하게 됨(이는 모델의 성능을 평가할 수 없게 되는 것)
- 모델은 train data에 있는 평균과 분산을 학습하게 되는데, 이렇게 학습된 scaler()의 파라미터는 test data를 스케일하는데 사용됨 --> train data로 학습된 scaler()의 파라미터를 통해 test data의 피쳐값들이 스케일 됨
#9 실습
coming..
'[Naver Cloud Camp 7] 교육 정리' 카테고리의 다른 글
| 네이버 클라우드 캠프 17일차 230517 (0) | 2023.05.20 |
|---|---|
| 네이버 클라우드 캠프 16일차 230516 (0) | 2023.05.16 |
| 네이버 클라우드 캠프 14일차 230512 (1) | 2023.05.12 |
| 네이버 클라우드 캠프 13일차 230511 (0) | 2023.05.11 |
| 네이버 클라우드 캠프 12일차 230510 (0) | 2023.05.10 |


